보드게임 '나크베의 보물'에서 발견한 수학

 

 보드게임 '나크베의 보물'은 주사위를 굴려 모험가를 골인 지점까지 탈출시키는 간단한 보드게임이다. 진행 방식이 윷놀이 내지 뱀과 사다리 게임과 유사하다고 보면 된다. 그러나 세부규칙에서 큰 차이가 있어 앞선 예시들과는 다른 재미를 느낄 수 있다. 

 

 이 보드게임이 가지는 가장 차별화되는 점은 (대개는 색깔로 구별된) 특정된 말이 없다는 것이다. 보드게임에서 움직이는 말은 총 7명인데, 그저 서로다른 개성의 모험가들일 뿐이다. 대신 이 게임엔 서로 다른 모험가 3명이 그려진 '후원자 카드'가 있다. 플레이어는 임의로 이 카드 한 장을 받고 어떤 모험가들이 그려져있는지 확인하고나서야 자기가 후원해야하는 말이 누구누구인지 결정이 된다. 카드는 비밀로 붙여, 다른 플레이어는 내가 누구를 후원하는 지 추측할 수 밖에 없다.

 

 더욱 흥미로운 점은 내가 플레이하는 말과 다른 플레이어가 후원하는 모험가 말이 같을 수도 있다는 것이다. 플레이어들은 상대의 후원자 말을 추측하는 과정 속에서 공통 모험가를 눈치껏 알아내어 연합을 짤 수도 있고, 혹은 상대가 공통 모험가를 지원하는 동안 나에게만 지정된 모험가를 몰아서 지원하므로써 내 후원자 카드에 적힌 모험가들의 평균 달리기가 모두 좋은 점수를 얻도록 전략을 짤 수도 있다.

 이 모든 것은 특별히 니 말 내 말이 정해지지 않고 후원자 카드를 통해서만 결정되기 때문에 그러하다.

 

 앞서 후원하는 모험가 말이 같을 '수도' 있다고 언급했는데, 해당 보드게임 작가인 라이너 크니지아(Reiner Knizia)는 더 신묘한 기술을 썼다. 그것은 어떤 후원자 카드 둘을 골라도 오직 한 명의 모험가만이 교집합에 있도록 만든 것이다.

 그렇다면 여기서 문제, 이 보드게임에서 후원자 카드는 모두 몇 개가 있을까? 각 카드는 어떤 구성을 하고 있을까? 카드에는 모두 세 명의 모험가가 담겨 있다.

 

정답

각 모험가들을 1234567로 부를 때, 모험가 카드는 총 일곱 장이며, 다음과 같은 구성을 하고있다.

125

137

236

146

567

247

345

 

겉보기에는 무작위로 선택된 것 처럼 보이고 정말 교집합이 하나인지 일일이 비교하며 확인해야 할 것 같지만, 이 상황을 대번에 정리하는 깔끔한 도식이 있다. 아래를 보라!

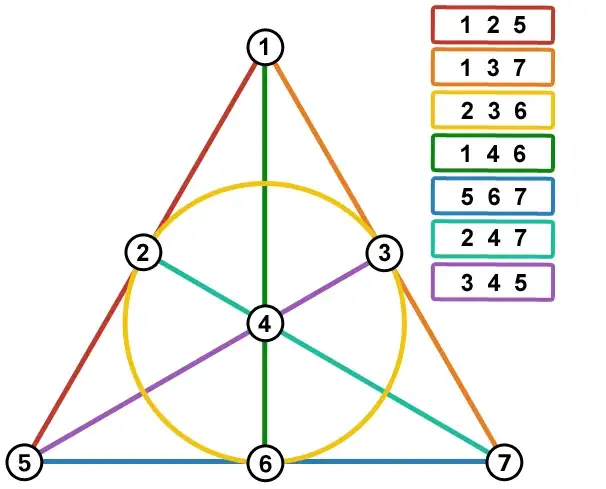
(출처: https://mickydore.medium.com/dobble-theory-and-implementation-ff21ddbb5318)

 

 해리포터 시리즈의 죽움의 성물 문양과도 닮은 이 그림에는 총 일곱개의 선이 있다. 정삼각형의 변을 이루는 세 선, 정삼각형의 세 수선, 그리고 내접원을 이루는 곡선이다. 정삼각형의 세 꼭짓점과 세 중점과 무게중심, 이렇게 총 일곱개의 점을 두고 앞서 언급한 선과의 관계를 살펴보면 언제나 정확히 한 점 만이 교차점이 된다는 것을 알 수 있다. 

 

 이와 같은 점과 선의 구성을 수학에서는 파노 평면(Fano Plane)이라 부른다. 위키피디아:

https://en.wikipedia.org/wiki/Fano_plane

 

 

 보드게임을 잘 아는 사람들이라면 앞서 언급한 내용에서 바로 Dobble(또는 Spot it!)이라는 게임을 떠올렸을 것이다. 이 게임은 아주 간단하다. 55개의 카드가 있고 각 카드에는 8개의 서로 다른 물건들이 그려져 있다. 임의의 두 카드가 공개되면 플레이어들은 재빨리 두 카드에 공통으로 들어있는 물건을 집어내야한다. 이 때, 어떤 두 카드를 공개하든, 두 카드에 모두 들어가있는 물건은 정확히 하나뿐이다.

 

 이런 특이한 조합의 카드를 이해하기 위해 우리는 Finite Projective Plane이라는 개념을 알면 좋다. Projective Plane은 점과 선으로 이루어진 객체로서, 어느 두 점을 골라도 오직 한 직선만이 그 둘을 지나고, 어느 두 선을 골라도 오직 한 점만이 두 직선 위에 있다. (플러스 다음 조건을 추가하면 된다: "어떤 네 점이 있어 어떤 선도 그 중 셋 이상을 지나지 못 한다.")

 

 이런 projective plane이 유한개의 점과 선으로 이루어져있으면 finite projective plane이라고 부른다. 나크베의 보물에 쓰인 파노 평면은 가장 작은 크기의 finite projective plane이다. Dobble의 경우 더 큰 크기의 finite projective plane을 쓴다고 생각하면 된다. 

 아래 Stand-up Maths 유튜브에 소개된 Dobble의 수학적 원리에 관한 영상 링크를 살펴보면 큰 도움이 될 것이다.

https://youtu.be/VTDKqW_GLkw

 

 또한 위 그림의 출처인 아래 Micky Dore의 설명또한 도움이 될 것이다.

https://mickydore.medium.com/dobble-theory-and-implementation-ff21ddbb5318

Dobble — Theory and Implementation