이 글에서 소개할 체스퍼즐은 환상적인 역행(Retrograde) 체스퍼즐들을 보여준 Raymond Smullyan의 작품이다. 그의 책 'The Chess Mysteries of Sherlock Holmes'의 초중반에 등장하는 퍼즐로, 뛰어난 완성도의 문제와 그에 곁들어진 홈즈의 퍼즐해설이 일품이라 하겠다.
책 내용은 소설의 형태를 띄고 있지만 이하 글에서는 간료하게 문제와 그 풀이를 제시한다.

흑이 위, 백이 아래에 자리잡고 경기 중이다. 그런데 시작 전, 체스에 필요한 32개의 말 중 하나가 분실되어서 사라진 기물을 동전으로 대체하여 게임을 진행했다고 한다. 그 동전이 그림의 h4에 있는 금색 동그라미라고 할 때, 사라진 기물은 무엇인가?
책 전반부에 수록된 퍼즐들 중 가장 화려하고 복합적인 풀이를 요구하는 문제로 난이도가 매우 높지만 체스규칙을 토대로 차근차근 추리해나가면 분명 답을 얻을 수 있을 것이다. 너무 당황하지 말기를, '불가능한 것들을 제외하고 남은 것이 뭐든, 아무리 사실 같지 않더라도 틀림없이 진실이다.'
정답과 풀이
정답은 백의 비숍이다.
먼저 주목할 것은 흑 킹이 백 룩에 의해 체크당해있다는 것이다. 당연히 백이 마지막에 둔 수로 체크가 일어났을텐데, 한 수 이전으로 역행했은 때는 흑의 체크당해있지 않아야한다. 직접 위협하고있는 d7의 백 룩이 역행할 수 있는 유일한 자리는 c7인데, 이 곳으로 가봤자 여전히 흑을 체크하므로 이 룩이 마지막으로 움직인 것이 아니다. 고로 백의 공격은 디스커버 체크를 통해 일어났으며, c7에서 어떤 백 기물이 움직여주었다는 것까지 알 수 있다.
그런데 판 위에 보이는 백 기물들은 킹과 폰들 그리고 두 룩 뿐이므로 동전이 백 기물이라고까지 가정해도 일반적인 움직임으로 c7에서 백 기물이 탈출할 수 없다. 생각할 수 있는 가능성은 기물이 본 모습과 다르게 움직였다는 것인데, 이를 잘 뜯어보면 본 모습이 다르다, 즉 원래 A의 규칙대로 움직이다가 어느 순간 B의 모습으로 바뀌었다고 추론할 수 있다. 왜냐하면 체스에는 그런게 가능하도록 하는 비일반적인 규칙이 있기 때문이다. 바로 '승격(promotion)'이다. c7에 있던 백 폰이 d8으로 움직이며 룩으로 승격한 것이다.
판 위에 이미 7개의 백 폰이 있으므로 마지막 수를 제외한 다른 승격은 없었음을 확인할 수 있다.

이제 승격이 있기 직전 상황으로 돌아가자.
백 폰이 대각선으로 움직이기 위해서는 흑 기물을 잡아햐한다. d8에 있었던 이 흑기물은 무엇일까? 가장 마지막 줄이라 폰은 절대 안되니 메이저 기물(major pieces)인 퀸, 룩이거나 마이너 기물(minor pieces)인 나이트, 비숍일 것이다.
이 기물이 메이저 기물인 퀸이나 룩이었다고 가정하자. 그러면 백 킹이 체크당하는 상황이라 한 번 더 역행했을 때 체크가 풀려야한다. d8 주변을 보면 승격될 백 폰을 비롯해 흑나이트, 백룩, 흑폰에 의해 둘러쌓여있으므로 d8에 있던 메이저 기물이 역행해봤자 다시 마지막줄이어서 체크를 벗어날 수 없다. 디스커버 체크를 상정해도 e8,f8,g8 자리로 역행할 수 있는 기물이 없다. 동전이 흑 기물이었다고 가정해도, 또 승격같은 비일반적인 행마를 고려해도 그렇다. 따라서 d8에 있던 흑기물은 메이저 기물이 아니다.
이제 이 기물이 마이너 기물인 나이트나 비숍임을 알았다. 만약 나이트였다면 판 위에 세 개의 나이트가 있게 되므로 이들중 하나가 흑 폰의 승격으로 만들어진 나이트여야한다. 만약 비숍이었다면 이 비숍은 반드시 흑 폰의 승격으로 만들어진 비숍이어야한다. 승격이 아닌 원 비숍이었을 경우, 이 비숍은 지금 검은 칸을 밟고 있기에 검은 칸 흑 비숍의 시작자리인 f8에서 출발해 d8에 당도해야하는데, f8자리가 한 번도 움직이지 않은 e7, g7의 두 폰에 의해 가로막혀있기 때문이다.
결국 d8의 흑기물이 어떤 마이너 기물이든 간에 흑이 한 번의 승격을 했음을 알 수 있다. 판 위에 이미 7개의 흑 폰이 있으므로 흑의 승격은 딱 한 번 뿐이었음까지 알 수 있다.
여기까지 오면 동전이 대체하고있는 기물이 흑인지 백인지 알 수 있다. 우선 흑기물이라고 가정하자.
-폰일 경우
이 경우 판 위에 8개의 폰이 모두 존재하므로 흑의 승격 횟수가 0이 된다. 앞선 논의에 의해 이는 불가능.
-메이저 기물(퀸, 룩)일 경우
이 경우 백이 체크상태에 놓인다. 마지막 순간 흑이 체크상태이고, 흑과 백이 동시에 체크당하는 일은 없기 때문에 이는 불가능.
-마이너 기물(나이트, 비숍)일 경우
이 경우 앞에서 했던 논리를 그대로 따라가면 흑의 승격이 또 한 번 발생해야한다. 흑의 승격은 딱 한 번 뿐이었으므로 이는 불가능.
따라서 어떤 경우든 이 기물은 흑의 것이 될 수 없다. 동전은 백의 기물을 대신하고 있는 것이다. 백도 승격이 한 번은 일어났으니 동전이 폰인 것은 아니다.
앞선 내용들을 정리해보자.
-백은 딱 한 번 폰을 승격시켰으며, 이를 통해 폰은 룩이 되었다.
(이 수는 가장 마지막 수였으며, c7에서 d8로 흑 기물을 잡으며 움직이는 수였기에 디스커버 체크가 되었다.)
-흑은 딱 한 번 폰을 승격시켰으며, 이를 통해 폰은 마이너기물(나이트, 비숍)이 되었다.
-동전이 대체 중인 사라진 기물은 백의 것이며, 퀸, 룩, 나이트, 비숍 중 하나이다.
앞으로 우리는 승격된 폰을 비롯해 폰들의 전반적인 움직임을 조사해 이 경기의 거시적인 흐름을 파악하고자 한다.
먼저 백 폰들 부터 분석하자.
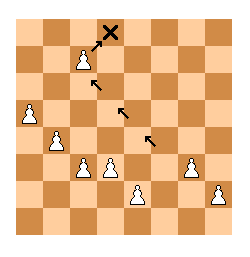
e2와 h2에 있는 폰들은 움직인 적이 없다. a5, b4, c3, d3 자리들은 오직 abcde열에서 시작한 폰들만이 접근할 수있으므로 abcd열 폰들이 a5, b4, c3, d3 자리의 폰들에 대응된다. 따라서 승격될 폰과 g3의 폰은 f2와 g2에 있던 두 폰에 대응된다.
c7에서 d8로 움직여 승격될 이 폰이 g2에 있던 폰이라면, c7까지 오기위해 최소 4번 흑 기물을 잡아야하고, 이후 최종적으로 d8으로 가며 한 번 더 흑 기물을 잡기 때문에 혼자서 최소한 5개의 기물을 잡았어야한다. 판 위의 흑 기물은 모두 10개이니 6개의 흑 기물이 잡혔는데, 이 중 검은 칸 흑 비숍은 제자리(f8)에서 잡혔으므로 남은 다섯 기물을 승격될 폰이 모두 잡은 셈이다. 그러면 f2에 폰이 g3로 기물을 잡으며 움직을 수가 없어 모순이다.
따라서 승격될 폰은 f2에서 출발한 폰이고, 자동적으로 g3에 있는 폰은 g2에서 출발해 한 칸 앞으로 갔다는 것도 알 수 있다.
다음 흑 폰들을 분석하자.
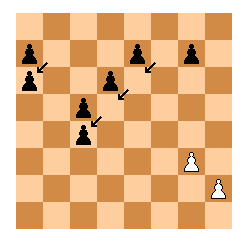
흑 폰의 경우 분석이 더 쉽다. a7,e7,g7의 폰들은 움직인 적이 없다. a6의 폰은 b7에서 왔고, c5,d6의 폰들은 cd열에서 시작한 폰들이여야해서 c4의 폰은 f7에서 출발했어야한다. 특히 이 폰은 f7에서 출발해 정확히 e6, d5를 거쳐 왔어야한다. 언급된 폰들을 제외하면 승격된 흑 폰은 h2에 있던 폰이 된다.
판 위에 백 기물은 동전을 포함해 모두 11개이니 5개의 백 기물이 잡혔는데, b열에서 출발한 폰이 하나를 잡고, f열에서 출발한 폰이 3개를 잡았으므로 h2에서 출발한 폰은 최대 하나만을 잡을 수 있다. 이 폰이 승격되기 위해서는 제일 앞 1열까지 와야하는데 h2의 백 폰이 수문장처럼 지키고있으므로 흑 폰은 정말로 백 기물을 딱 하나 잡아 g열을 이동했어야한다. 특히 g3를 지키는 백 폰은 g2에서 왔으므로 흑 폰의 유일한 통로는 h3에서 g2로 움직이는 것 뿐이다.
이제 마무리할 때가 왔다.
백의 사라진 다섯 기물은 모두 흑 폰들에 의해 붙잡혔으며 그 위치가 정확히 a6, c4, d5, e6, g2이다. 이들은 모두 공통적으로 하얀 칸이다. 백은 마지막 수를 제외하면 승격한 적이 없으므로 붙잡힌 기물들은 모두 폰이 아닌 원 기물들이다. 이들 중 하얀 칸으로 움직여 흑에 잡힐 수 있는 것은 퀸, 룩, 나이트, 하얀 칸 비숍이며, 검은 칸 비숍은 어떤 경우에도 하얀 칸으로 이동할 수 없다. 따라서 판 위에 남아있어야만 하는 백 기물은 검은 칸에서 출발한 비숍이며, 이것이 곧 동전이 대체하고 있는 사라진 기물이다.
'게임과 퍼즐 > 체스 퍼즐' 카테고리의 다른 글
| 백 킹은 어디에 있는가? (0) | 2019.01.20 |
|---|---|
| Don't Mate in One (0) | 2018.01.20 |
| 체스 최대배치문제 - 나이트편 (0) | 2017.09.19 |
| 체스 최대배치문제 - 비숍편 (0) | 2017.09.17 |
| 나이트 일주 5×5 (2) | 2016.09.04 |



