이 글을 쓰는 지금은 코로나 시국, 사회적 거리두기 캠페인이 한창이다. 이번 글에서는 거리두기와 관련있는 경우의 수 문제를 준비해보았다. 좀 어려운 경우의 수 문제를 자주 접해본 고등학생들이라면 이미 풀어봤을 법한, 그런 잘 알려진 문제이다.

|
1. 세 명의 사람과 일렬로 나열된 8개의 좌석이 있다. 이 중 세 좌석을 골라 앉되 어떤 두 사람 사이에도 최소 한 좌석은 비어있어야 할 때, 세 사람이 앉을 수 있는 경우의 수는 모두 몇인가? 2. 세 명의 사람과 원탁에 배치된 8개의 돠석이 있다. 이 중 세 좌석을 골라 앉되 어떤 두 사람 사이에도 최소 한 좌석은 비어있어야 할 때, 세 사람이 앉을 수 있는 경우의 수는 모두 몇인가? (주의! 원탁에 앉는 경우의 수를 구할 땐 회전에서 같아지면 모두 하나로 센다.) |
힌트: 문제를 쉽게 만드는 다른 경우의 수를 찾아 조합적 증명(Combinatorial proof)을 써라!
풀이
정답은 120, 12이다.
이 문제는 두 사람 사이의 빈자리를 의식하면 계산하기가 복잡해진다. 문제를 푸는 간단한 방법은 서로를 띄어놓을 두 자리를 미리 빼놓는 것이다. 그러면 총 여섯 좌석이 남는데, 여기에 세 사람이 아무렇게나 앉은 뒤 사람 사이에 빼놓은 좌석을 다시 채워놓으면 그만이다.
아래 그림은 좌석을 빼기 전과 채운 후의 일대일 대응을 보여준다.
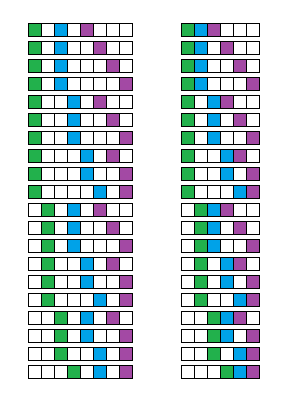
결국 이 문제는 여섯 좌석에서 세사람이 앉을 세 좌석을 뽑는 간단한 문제가 된다. 답은 6×5×4=120.
2. 원탁의 경우도 마찬가지이다. 다만 이 때는 정확히 사람 수 만큼 좌석을 빼야 할 것이다. 그러면 해당 문제는 다섯 좌석 원탁에 세 사람이 앉는 경우의 수와 같다. 이는 (5×4×3)÷5=12.
'조합론 퍼즐' 카테고리의 다른 글
| 3×1 조각으로 체스판 채우기(feat.소사이어티게임2 10화) (0) | 2017.10.28 |
|---|---|
| 이항정리의 따름정리들과 조합적 증명 (2) | 2017.10.15 |
| 보안을 위한 자물쇠의 개수는? (0) | 2017.04.16 |
| 체스판 위에 도미노 깔기 2 (0) | 2013.04.14 |
| 귀퉁이 잘린 체스판에 도미노 깔기 (0) | 2013.04.01 |



