
좌표공간 위의 개미가 원점에서 출발해 다음과 같은 규칙으로 움직이려고한다.
1. 처음엔 오른쪽으로 1칸 전진하고 다음부터 이전에 전진한 길이에 1을 더한 만큼 더 전진한다.
2. 한 번 전진한 이후 좌회전 또는 우회전으로 90도 꺾어 움직인다.
3. 전에 걸었던 길을 또 밟지 않는다.
예를 들면 다음과 같다. 개미가 원점에서 오른쪽으로 1칸 전진했다고 하자. 다음은 위쪽 또는 아래쪽으로 2칸 전진한다. 그, 다음은 왼쪽 또는 오른쪽으로 3칸 전진한다. 이후 다시 90도 꺾어 4칸 전진하고, 그 다음 계속 같은 규칙을 반복한다.
만약 개미가 규칙을 따라 움직이다가 세로 움직임 이후(즉 위쪽으로 움직이거나 아래쪽으로 움직여서) 제자리로(=원점으로) 돌아왔다고 가정하자. 그러면 그 경로를 테두리로 이루는 도형을 찾을 수 있는데, 이를 골리곤(Golygon)이라 부르도록 하자. 규칙에 따르면 골리곤은 모든 내각이 90도 또는 270도이면서 변의 길이가 1부터 연속된 자연수를 이루는 도형이 된다.
그렇다면 질문. 골리곤은 존재하는가? 존재한다면 가장 작은 크기의 골리곤을 찾아라. 존재하지 않는다면 증명해보아라.
+골리곤이 존재한다면 변의 개수는 얼마여야하는지도 생각해보자.
정답 및 풀이
골리곤은 존재하며, 가장 작은 크기의 골리곤은 8개의 변을 가진다.
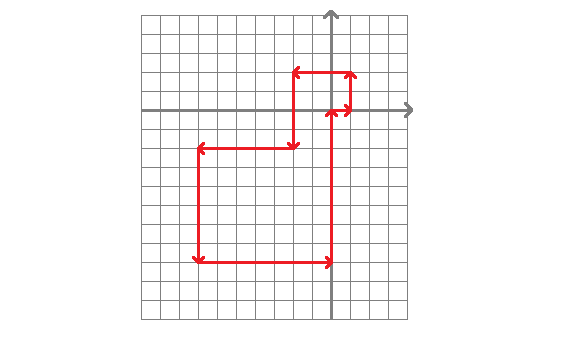
자세히 말하자면, 골리곤은 변의 개수가 오직 8의 배수일때만 존재한다는 것이 알려져있다. 아래 논문을 인용하여, 이 정리를 간단히 설명해보려고 한다.
먼저 골리곤의 변의 개수는 아무리 못해도 4배수 형태여야한다는 것을 증명한다.
개미와 좌표평면대신 거대한 체스판과 룩을 생각하자. 룩은 홀수길이 움직임에서는 다른 색깔을 칸을 밟고 짝수길이 움직에서는 같은 색깔의 칸을 밟는다. 따라서 이 룩이 백칸에서 출발한다면 순서대로 흑흑백백흑흑백백...순으로 체스판 위 칸들을 밟게 된다. 최후에 세로움직임 이후 백칸 원점으로 돌아와야하므로 행마의 횟수는 4배수가 되어야한다.
이제 골리곤의 변의 개수는 8배수 형태여야한다는 것을 증명한다.
이를위해 개미의 경로를 홀짝으로 나누어 생각할 필요가 있다. 개미가 홀수 길이를 걸을 때는 반드시 가로로 움직이고, 짝수 길이를 걸을 때는 세로로 움직인다. 두 움직임을 직교하므로 서로가 서로에게 영향을 주지 않는다. 따라서 개미가 n차례 움직여 원점에 도착했다면, 가로움직임과 세로움직임을 따로 계산해서 둘 다 0이 나와야한다. 즉,
±1±3±5±...±(n-1)=0
±2±4±6±...±n=0
과 같은 두 방정식을 +-를 적당히 골라 만족시켜야 한다. +는 양의 방향(오른쪽 또는 위), -는 음의 방향(왼쪽 또는 아래)을 상징한다고 보면 된다.
앞서 n에 4배수라 하였으므로 n=4k로 두자. 두 번째 식에서 4k보다 작은 모든 짝수들을 정리해 +계열 짝수들의 합과 -계열 짝수들의 합이 같아야한다. 4k보다 작은 모든 짝수들의 합은,
2+4+...+4k = 2(1+2+...+2k) = 2×(2k(2k+1)/2) = 2k(2k+1)
이므로 +계열 짝수들의 합과 -계열 짝수들의 합은 k(2k+1)로 동일하다. 그런데 짝수들의 합은 언제나 다시 짝수이므로 k(2k+1)은 짝수여야한다. 2k+1이 항상 홀수이므로 k가 짝수여야하고, 결론적으로 n=4k는 실은 8배수여야한다.
마지막으로 n이 8배수이면 항상 골리곤을 만들 수 있음을 보인다.
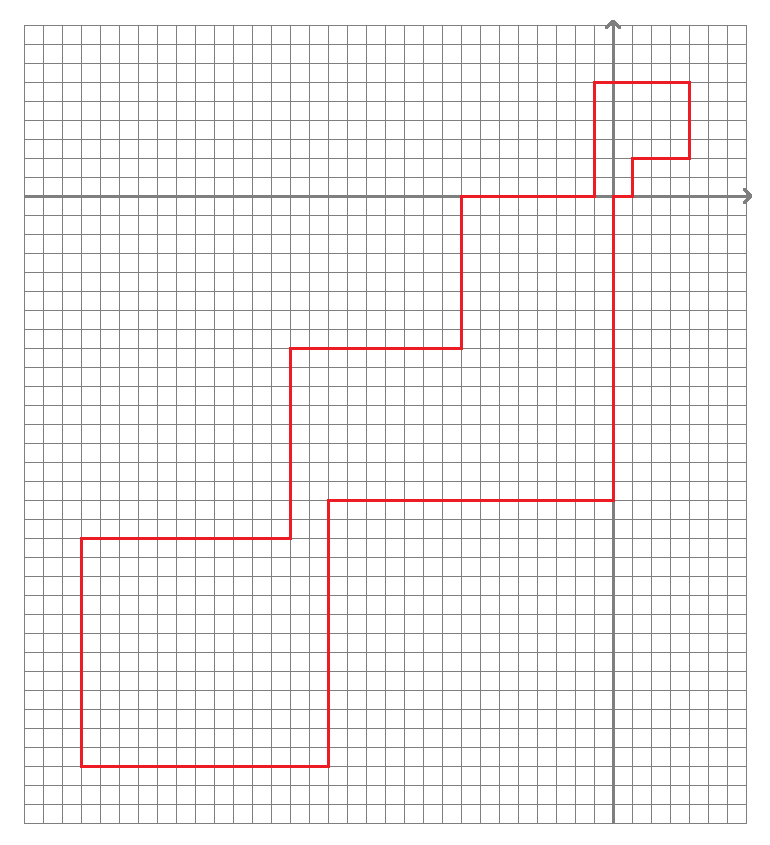
1부터 n까지 자연수들 중 앞 1/4과 뒤 1/4에 +를, 나머지엔 -를 배정한다. 이를테면 n=16이면
+1+2+3+4-5-6-7-8-9-10-11-12+13+14+15+16
과 같이 배정한다. 이 때 홀수들이 +인 것을 오른쪽 뱡향을, 짝수들이 +인 것은 위쪽 방향을 의미한다.
배정된 뱡향에 따라 진행하면 기울기의 크기때문에(2/1>4/3>6/5>8/7>...>16/15>1)개미의 경로가 아슬아슬하게 겹치지 않는다는 것을 쉽게 확인할 수 있다.
※Lee Sallows의 문제입니다. 골리곤에 대한 설명은 아래 Wikipedia 또는 Mathworld에서 확인할 수 있습니다.
https://en.wikipedia.org/wiki/Golygon
https://mathworld.wolfram.com/Golygon.html
골리곤에 대한 수학적 증명은 아래 논문에서 확인할 수 있습니다.
https://www.leesallows.com/files/SS%20Isogons%20of%2090%20Degrees.pdf